16-01-2013, 1:02 PM
Se conoce como binomio de Newton al método que permite hallar la potencia de un binomio elevado a una variable.
$$ (a ± b)^{n}, n∈ℕ $$
Veamos los siguientes ejemplos:
\( (a + b)^{0} = 1 \)
\( (a + b)^{1} = 1·a + 1·b \)
\( (a + b)^{2} = 1·a^2 + 2·a·b + 1·b^2 \)
\( (a + b)^{3} = 1·x^3 + 3·x^3·y + 3·x·y^3 + 1·y^3 \)
\( ... \)
Como vemos, para los determinados valores de \( n \) los coeficientes son diferentes.
\( n = 0 \Rightarrow \left\{ 1 \right\} \)
\( n = 1 \Rightarrow \left\{ 1, 1 \right\} \)
\( n = 2 \Rightarrow \left\{ 1, 2, 1 \right\} \)
\( n = 3 \Rightarrow \left\{ 1, 3, 3, 1 \right\} \)
\( ... \)
Los coeficientes no son al azar, sino que siguen un orden determinados, el cual recibe el nombre de triángulo de Pascal (a veces conocido como triángulo de Tartaglia):

Construcción del triángulo de Pascal:
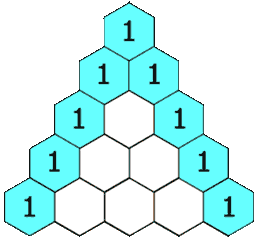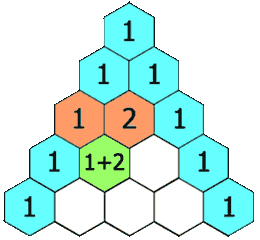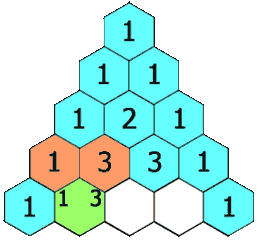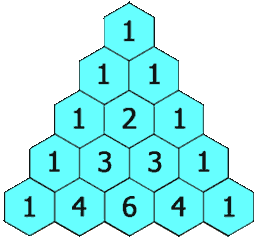
Cada número en el triángulo es la suma de los dos que están situados por encima de el.
No es necesario hacer 16 líneas del triángulo de Pascal para conocer los coeficientes de un binomio elevado a la 15, hoy en día, gracias a los números combinatorios (y más específicamente a Newton por deducir la fórmula), podemos conocerlos analíticamente.
Fórmula del binomio de Newton:
$$ (x+y)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} x^{n-k} y^k $$
¿Cómo calcularlo columna y fila en la calculadora científica?
Como siempre digo, todo varía dependiendo de la marca y del modelo, basándome en la calculadora científica de CASIO modelo fx-95MS:
F + nCr + C =
Siendo:
· C = número de columna.
· F = número de fila.
Ejemplo:
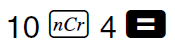
El resultado sería: 210.
$$ (a ± b)^{n}, n∈ℕ $$
Veamos los siguientes ejemplos:
\( (a + b)^{0} = 1 \)
\( (a + b)^{1} = 1·a + 1·b \)
\( (a + b)^{2} = 1·a^2 + 2·a·b + 1·b^2 \)
\( (a + b)^{3} = 1·x^3 + 3·x^3·y + 3·x·y^3 + 1·y^3 \)
\( ... \)
Como vemos, para los determinados valores de \( n \) los coeficientes son diferentes.
\( n = 0 \Rightarrow \left\{ 1 \right\} \)
\( n = 1 \Rightarrow \left\{ 1, 1 \right\} \)
\( n = 2 \Rightarrow \left\{ 1, 2, 1 \right\} \)
\( n = 3 \Rightarrow \left\{ 1, 3, 3, 1 \right\} \)
\( ... \)
Los coeficientes no son al azar, sino que siguen un orden determinados, el cual recibe el nombre de triángulo de Pascal (a veces conocido como triángulo de Tartaglia):

Quote
Los coeficientes de la forma desarrollada de \( (a ± b)^{n} \) se encuentran en la línea \( n + 1 \) del triángulo de Pascal.
Quote
Todo binomio de la forma \( (a ± b)^{n} \) tiene \( n + 1 \) términos diferentes.
Construcción del triángulo de Pascal:

Cada número en el triángulo es la suma de los dos que están situados por encima de el.
No es necesario hacer 16 líneas del triángulo de Pascal para conocer los coeficientes de un binomio elevado a la 15, hoy en día, gracias a los números combinatorios (y más específicamente a Newton por deducir la fórmula), podemos conocerlos analíticamente.
Fórmula del binomio de Newton:
$$ (x+y)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} x^{n-k} y^k $$
¿Cómo calcularlo columna y fila en la calculadora científica?
Como siempre digo, todo varía dependiendo de la marca y del modelo, basándome en la calculadora científica de CASIO modelo fx-95MS:
F + nCr + C =
Siendo:
· C = número de columna.
· F = número de fila.
Quote
Tener en cuenta que tanto las filas como las columnas se empiezan a contar desde 0.
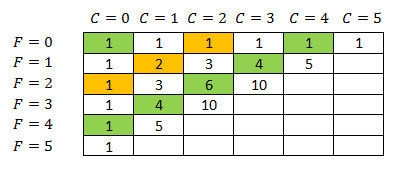
La fila es el valor de \( n \) y la columna es el lugar del coeficiente.

La fila es el valor de \( n \) y la columna es el lugar del coeficiente.
Ejemplo:
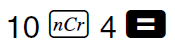
El resultado sería: 210.