|
Problema de M.R.U.V.
|
|
1. La siguiente tabla proporciona valores, para varios instantes, de la velocidad de un móvil que se desplaza en linea recta, determine:
t(s) 1,0 2,0 3,0 4,0 5,0
v(m/s) 5,0 8,0 11,0 14,0 17,0
Nota: si la tabla se ve dispareja tomen que (1,0 esta arriba de 5,0 y así sucesivamente).
a. ¿Qué clase de movimiento mantiene el móvil?
b. ¿Cuál es el valor de su aceleración?
c. ¿Cuál es la velocidad inicial del móvil?
d. ¿Qué distancia recorre el móvil desde t=0,0 hasta t=4,0 s?
e. ¿Cuál es la ecuación de la posición para cualquier tiempo t?
f. Realice la gráfica cuantitativa de la posición en función del tiempo.
2. Una persona le proporciona la siguiente ecuación del movimiento a un objeto que se desplaza en linea recta:
$$ x_{1}=6.0t + 2.5t^2 $$
donde t se halla en (s) y x en (m). Basándose en esta información, determine:
a. El tipo de movimiento del cuerpo.
b. Si en el mismo instante en que este objeto inicia su movimiento, otro objeto comienza su recorrido desde \( x_{2}=5.0 + 3.0t \), realice una gráfica de las posiciones en función del tiempo.
c. ¿En que tiempo t ambos se encuentran en la misma posición?
3. Un auto y un colectivo están ubicados a una distancia de 100m y se mueven a 55 y 25 km/h respectivamente.
a. Calcule cuanto tiempo tardan en encontrarse
b. Halle el lugar donde se encuentran.
c. Haga el gráfico de x(t) para los dos móviles y verifique los puntos a y b.
|
Quote 1. La siguiente tabla proporciona valores, para varios instantes, de la velocidad de un móvil que se desplaza en linea recta, determine:
t(s) 1,0 2,0 3,0 4,0 5,0
v(m/s) 5,0 8,0 11,0 14,0 17,0
Nota: si la tabla se ve dispareja tomen que (1,0 esta arriba de 5,0 y así sucesivamente).
a. ¿Qué clase de movimiento mantiene el móvil?
b. ¿Cuál es el valor de su aceleración?
c. ¿Cuál es la velocidad inicial del móvil?
d. ¿Qué distancia recorre el móvil desde t=0,0 hasta t=4,0 s?
e. ¿Cuál es la ecuación de la posición para cualquier tiempo t?
f. Realice la gráfica cuantitativa de la posición en función del tiempo.
a. Como vemos que la velocidad varía, estamos en presencia de M.R.U.V.
b. Para calcular la aceleración, utilizaré la siguiente fórmula:
$$ a = \frac {\Delta v}{\Delta t} \Rightarrow a = \frac {v_{f} - v_{i}}{t_{f} - t_{i}} \Rightarrow a = \frac {17,0 \frac {m}{s} - 5,0 \frac {m}{s}}{5,0 s - 1,0 s} = \frac {12,0 \frac {m}{s}}{4,0 s} = 3,0 \frac {m}{s^2} $$
c. Para calcular la velocidad inicial del móvil, utilizaré la siguiente fórmula:
$$ v_{f} = v_{i} + a · \Delta t \Rightarrow v_{i} = v_{f} - a · \Delta t \Rightarrow v_{i} = 17,0 \frac {m}{s} - 3,0 \frac {m}{s^2} · 5,0 s = 2,0 \frac {m}{s} $$
d. Para hallar la distancia recorrida por el móvil, utilizaré la siguiente fórmula:
$$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} \Rightarrow x_{f} = 0,0 m + 2,0 \frac {m}{s} · (4,0 s - 0,0 s) + \frac {3,0 \frac {m}{s^2} · (4,0 s - 0,0 s)^2}{2} = 32,0 m$$
e. Para escribir la ecuación de posición, para cualquier valor de t, utilizaré la anterior fórmula:
$$ x_{f} = 0,0 m + 2,0 \frac {m}{s}· \Delta t + \frac {3,0 \frac {m}{s^2} · \Delta t^2}{2} $$
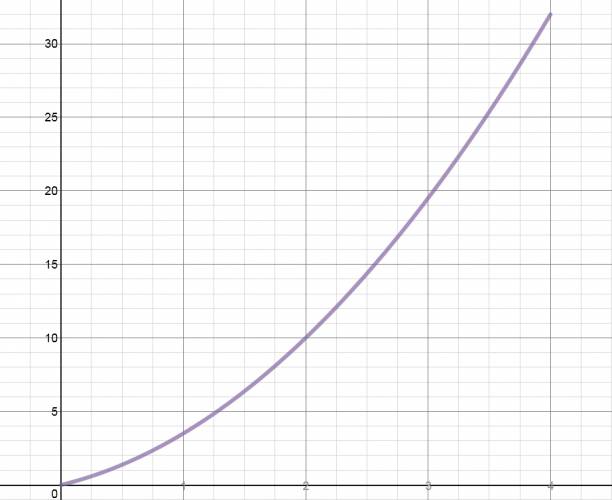
f. La gráfica de posición en función de tiempo \( x(t) \), sería algo así:
|
Quote (marcos364) 2. Una persona le proporciona la siguiente ecuación del movimiento a un objeto que se desplaza en linea recta:
$$ x_{1} = 6.0t+2.5t^2 $$
donde t se halla en (s) y x en (m). Basándose en esta información, determine:
a. El tipo de movimiento del cuerpo.
b. Si en el mismo instante en que este objeto inicia su movimiento, otro objeto comienza su recorrido desde \( x_{2} = 5.0+3.0t \), realice una gráfica de las posiciones en función del tiempo.
c. ¿En que tiempo t ambos se encuentran en la misma posición?
a. Sólo con ver la ecuación puedo decir que como el tiempo se encuentra al cuadrado: es un movimiento acelerado (entiéndase M.R.U.V.).
b. La gráfica de posición en función de tiempo de ambos movimientos sería algo así:
c. El momento de encuentro lo podemos obtener directamente del gráfico, pero sé que es antes de un segundo, pero no sé exactamente cuándo, por esta razón lo haré analíticamente.
Igualo ambos movimientos:
\( x_{1}=6.0t + 2.5t^2 \)
\( x_{2}=5.0 + 3.0t \)
$$ 6.0t + 2.5t^2 = 5.0 + 3.0t \Rightarrow 2,5·t^2 + 3·t - 5 = 0 $$
Resuelvo la anterior ecuación por Bháskara y llego a las siguientes raíces:
$$ S = \left\{ \frac {-3 + \sqrt{59}}{5}; \frac {-3 - \sqrt{59}}{5}\right\} $$
Los tiempos no pueden ser negativos, por lo que nos quedamos con: \( \frac {-3 + \sqrt{59}}{5} = 0,94 s \)
Los móviles se encontrarán a los 0,94 s. |
Quote (marcos364) 3. Un auto y un colectivo están ubicados a una distancia de 100m y se mueven a 55 y 25 km/h respectivamente.
a. Calcule cuanto tiempo tardan en encontrarse
b. Halle el lugar donde se encuentran.
c. Haga el gráfico de x(t) para los dos móviles y verifique los puntos a y b.
El ejercicio no lo aclara, pero creeré que es M.R.U.:
a. Como en todo problema de encuentro, partimos de la fórmula, ponemos los datos y despejamos:
MÓVIL 1:
$$ v_{x} = \frac {\Delta x}{\Delta t} \Rightarrow 55 \frac {km}{h} = \frac {x_{f} - 0}{t_{f} - 0} \Rightarrow 55 \frac {km}{h} · t_{f} = x_{f} $$
MÓVIL 2:
$$ v_{x} = \frac {\Delta x}{\Delta t} \Rightarrow 25 \frac {km}{h} = \frac {x_{f} - 0,1 km}{t_{f} - 0} \Rightarrow 25 \frac {km}{h} · t_{f} + 0,1 km = x_{f} $$
Igualo las anteriores ecuaciones:
$$ 55 \frac {km}{h} · t_{f} = 25 \frac {km}{h} · t_{f} + 0,1 km \Rightarrow 55 \frac {km}{h} · t_{f} - 25 \frac {km}{h} · t_{f} = 0,1 km \Rightarrow 30 \frac {km}{h} · t_{f} = 0,1 km \Rightarrow t_{f} = \frac {0,1 km}{30 \frac {km}{h}} = 3,3·10^{-3} h $$
Serían casi 12 segundos.
b. Sustituyo en cualquiera de las dos ecuaciones:
$$ 55 \frac {km}{h} · t_{f} = x_{f} \Rightarrow 55 \frac {km}{h} · 3,3·10^{-3} h = 0,18 km $$
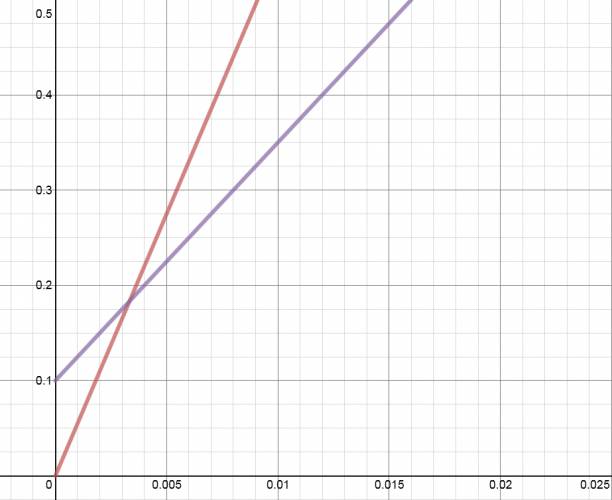
c. El gráfico sería algo así:
|
Muchas gracias por tomarte el trabajo y resolverlos. De verdad que me viene muy bien.. ya en poquito rindo y trato de tener la mayoría de problemas resueltos. Cuanto mas practica, mejor
Muchas gracias!
|
Quote (Ovale) Muchas gracias por tomarte el trabajo y resolverlos. De verdad que me viene muy bien.. ya en poquito rindo y trato de tener la mayoría de problemas resueltos. Cuanto mas practica, mejor
Muchas gracias!
Gracias a ti por darle sentido a mi tarea, si nadie lo necesitara no tendría sentido todo esto, la razón del foro es el poder ayudar, que cada uno dé de su parte para un bien mayor.  |