| Foro Problemas resueltos Problema de lanzamiento de proyectiles, desde la altura máxi |
| Problema de lanzamiento de proyectiles, desde la altura máxi |
09-12-2012, 7:50 PM
|
15-12-2012, 8:16 PM
|
15-12-2012, 8:20 PM
Quote (Flor) en este caso tengo que usar la ecuación esta h=g . delta t al cuadrado sobre 2 Exactamente, debes usar esa fórmula.  |
15-12-2012, 8:31 PM
otro
 |
15-12-2012, 8:39 PM
Hola Flor,
Creo que tuviste unas confusiones en este último:  Resolución: Como se lanza horizontalmente, ya conocemos la velocidad en el eje horizontal, que es constante (no varía en ningún momento). Para conocer el valor de la velocidad en el eje x, utilizaremos la fórmula de M.R.U.: $$ v_{x} = \frac {\Delta x}{\Delta t} = \frac {5,11 m}{0,9 s} = 5,7 \frac {m}{s} $$ Para hallar la velocidad en el eje vertical (eje y), utilizaremos la fórmula: $$ v_{f} = v_{i} - g· \Delta t $$ Dijimos que la velocidad inicial en el eje vertical es nula. Ahora sustituimos lo que conocemos en la fórmula y así hallar la velocidad final. 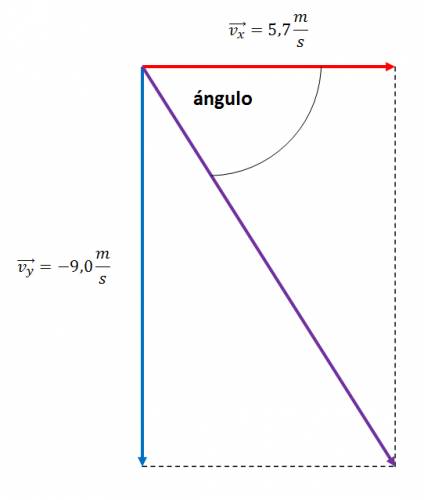$$ v_{f} = 0 \frac {m}{s} - 10 \frac {m}{s^2}· 0,9 s \Rightarrow v_{f} = - 9,0 \frac {m}{s} $$ Ahora sabemos que: Velocidad en el momento de impacto en el eje x: · \( v_{x} = 5,7 \frac {m}{s} \) Velocidad en el momento de impacto en el eje y: · \( v_{y} = - 9,0 \frac {m}{s} \) Hago un diagrama para que quede más claro:  Como la velocidad \( v_{x} \) y \( v_{y} \) son perpendiculares, para hallar la velocidad resultante, utilizaré el teorema de Pitágoras. 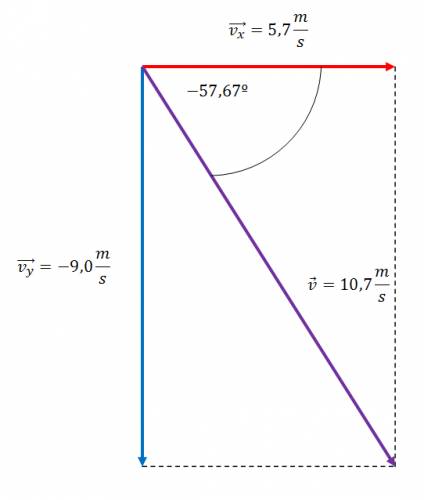$$ v = \sqrt { (v_{x})^2 + (v_{y})^2 } $$ $$ v = \sqrt { (5,7 \frac {m}{s})^2 + (-9,0 \frac {m}{s})^2 } $$ $$ v = 10,7 \frac {m}{s} $$ Ahora hallaré el ángulo de inclinación de la velocidad resultante, que llamaré \( \beta \): $$ tg \beta = \frac {v_{y}}{v_{x}} = \frac {-9,0 \frac {m}{s}}{5,7 \frac {m}{s}} = -1,58 $$ Lo que hicimos fue hallar la tangente del ángulo, para finalmente conocer el valor del ángulo, debemos hacer la función opuesta a la tangente que es el arcotangente: $$ \beta = arctg(-1,58) = -57,67 º $$ Quote Atención: Es correcto que el ángulo sea negativo, ya que este está por debajo de la velocidad horizontal.  |
15-12-2012, 8:47 PM
|
15-12-2012, 8:48 PM
Quote (Flor) o cea que tengo que buscar la vx porque no tiene velocidad en el eje y Exacto. |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.