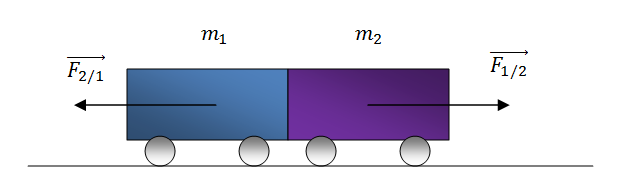
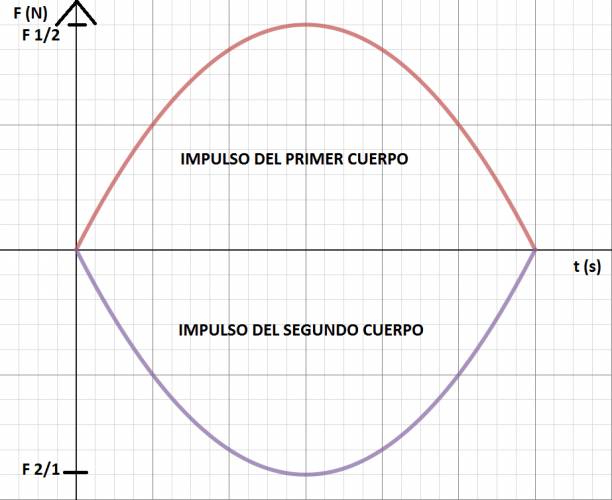
08-12-2012, 10:13 PM
Partimos de la segundo ley de Newton:
\( F = m·a \), pero sabemos que \( a = \frac {\Delta v}{\Delta t} \), por lo que sustituimos en la primer fórmula y nos queda que: \( F = m·\frac {\Delta v}{\Delta t} \), ahora despejamos: \( \vec F\cdot\bigtriangleup t= \bigtriangleup\vec p \)
Impulso:
Es la aplicación de una fuerza durante un periodo de tiempo.
$$ I = F· \Delta t $$
Unidad:
$$ \left [ N·s \right ] $$
Cantidad de movimiento:
Cuando se aplica el mismo impulso sobre cuerpos de distintas masas, experimentará una mayor velocidad el que posea una masa menor.
La cantidad de movimiento de un cuerpo es el producto de su masa por su velocidad.
$$ p = m· v $$
Unidad:
$$ \left [ kg· \frac{m}{s} \right ] $$
Tenemos que:
$$ I = \Delta p $$
\( F = m·a \), pero sabemos que \( a = \frac {\Delta v}{\Delta t} \), por lo que sustituimos en la primer fórmula y nos queda que: \( F = m·\frac {\Delta v}{\Delta t} \), ahora despejamos: \( \vec F\cdot\bigtriangleup t= \bigtriangleup\vec p \)
Impulso:
Es la aplicación de una fuerza durante un periodo de tiempo.
$$ I = F· \Delta t $$
Unidad:
$$ \left [ N·s \right ] $$
Cantidad de movimiento:
Cuando se aplica el mismo impulso sobre cuerpos de distintas masas, experimentará una mayor velocidad el que posea una masa menor.
La cantidad de movimiento de un cuerpo es el producto de su masa por su velocidad.
$$ p = m· v $$
Unidad:
$$ \left [ kg· \frac{m}{s} \right ] $$
Tenemos que:
$$ I = \Delta p $$