Universo Científico :: Problemas de movimiento (M.R.U.)

Página 1 de 1
1

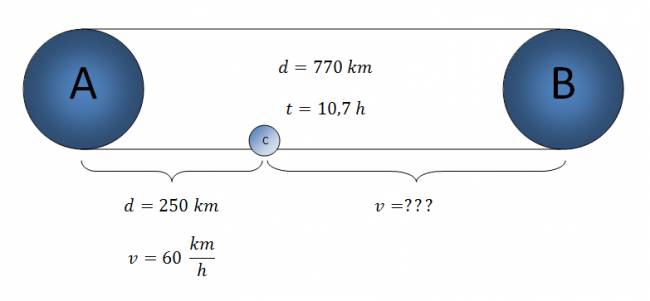
1. Un automovilista parte de una ciudad A hacia una ciudad B distante 770 km. Si recorre los primeros 250 km con una rapidez media de 60 km/h, ¿qué rapidez media debe desarrollar en el resto del recorrido si debe emplear 10 hr 40 min en ir de A hasta B?

2. Un automóvil parte de una ciudad A con una rapidez media de 50 km/h. Una hora y media después sale un segundo automóvil sobre la misma carretera y da alcance al primero después de transcurridas 2 horas. ¿Qué rapidez media desarrollo el segundo automóvil para alcanzar el primero?

Quote

Primero que nada tratemos de entender lo que dice el problema:

Dos ciudades A y B están separadas 770 km, en medio de estas ciudades hay una ciudad más pequeña C, la distancia entre A y C es de 250 km, los cuales, el automovilista recorrió con una velocidad de 60 km/h. Conociendo todo esto, debemos hallar el valor de la velocidad que tuvo entre la ciudad C y B.

Comencemos con los planteos:

Primero que nada, vamos a hallar el tiempo que demoró en ir de A hasta C:

$$ v_{x} = \frac {\Delta x}{\Delta t} \Rightarrow v_{x} = \frac {250 km}{60 \frac {km}{h}} = 4,2 h $$

Sabemos que la distancia entre A y B es 770 km, pero lo que nos interesa es la distancia entre C y B:
$$ \overline {AB} = \overline {AC} + \overline {CB} \Rightarrow 770 km = 250 km + \overline {CB} \Rightarrow \overline {CB} = 770 km - 250 km = 520 km$$

Lo mismo deducimos del tiempo: si al tiempo total (AB) se le resta el tiempo en el tramo AC, tendremos el tiempo en el tramo CB.

Por lo cual, el tiempo en el tramo CB es de: 6,4 h.

Ahora conocemos el tiempo y el desplazamiento de CB, simplemente hallamos la velocidad:

$$ v_{x} = \frac {\Delta x}{\Delta t} = \frac {520 km}{6,4 h} = 81,3 \frac {km}{h} $$

Quote

2. Un automóvil parte de una ciudad A con una rapidez media de 50 km/h. Una hora y media después sale un segundo automóvil sobre la misma carretera y da alcance al primero después de transcurridas 2 horas. ¿Qué rapidez media desarrollo el segundo automóvil para alcanzar el primero?

Explicación del problema:
Un automóvil se mueve con una velocidad de 50 km/h durante 3,75 h. Luego de una 1,5 h; parte otro automóvil que procura alcanzar al primero, y lo logra: a las 3,75 h. Se nos pide calcular la velocidad del segundo automóvil.

Como es un problema de encuentro planteamos las fórmulas para cada automóvil:

PRIMER AUTOMÓVIL:
$$ v_{x} = \frac {\Delta x}{\Delta t} \Rightarrow 50 \frac {km}{h} = \frac {x_{f} - 0 km}{3,5 h - 0} \Rightarrow x_{f} = 175 km $$

SEGUNDO AUTOMÓVIL:
$$ v_{x} = \frac {\Delta x}{\Delta t} \Rightarrow v = \frac {x_{f} - 0 km}{3,5 h - 1,5 h} \Rightarrow x_{f} = (2 h)·v $$

Ahora como $ x_{f} $ es la misma, en ambas ecuación, simplemente sustituimos, y nos queda que:

$$ 175 km = (2 h) · v \Rightarrow v = \frac {175 km}{2 h} = 87,5 \frac {km}{h} $$

Página 1 de 1
1

Universo Científico

marcos364

Admin

Admin