| Foro Problemas resueltos Problema de proyectiles, se conoce altura y alcance |
| Problema de proyectiles, se conoce altura y alcance |
02-12-2012, 9:20 PM
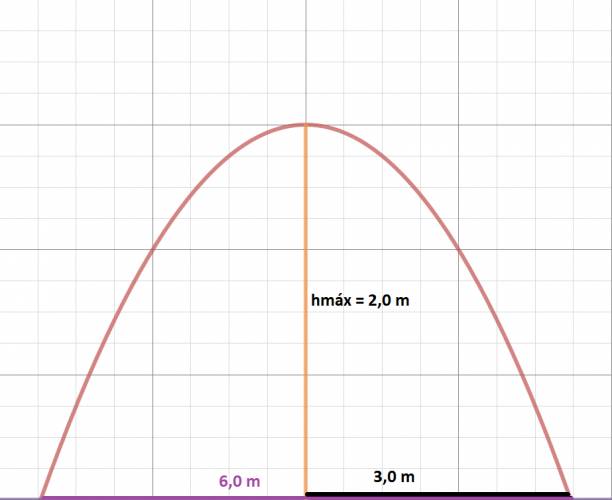
 De un proyectil se conoce su altura máxima que es de 2,0 m; y la distancia desde la altura máxima hasta que el suelo que es de 3,0 m; como se muestra en la figura, el recorrido del proyectil se encuentra marcado con rojo. Determinar la velocidad con la que fue lanzado y el ángulo con respecto a la horizontal. |
02-12-2012, 9:26 PM
 Rápidamente deducimos el alcance del proyectil: sabemos que la distancia de cualquiera de los extremos a la altura máxima es la mitad, por lo que el alcance del proyectil es de 6,0 m. Aplicamos la fórmula de altura para conocer el tiempo: \( x_{f} = x_{i} + v_{o}· \Delta t - \frac {g· \Delta t^2}{2} \) Pero sabemos que \(v_{o} = 0 \) porque se encuentra en la altura máxima, por lo que nos queda que: \( x_{f} = x_{i} - \frac {g· \Delta t^2}{2} \) Ahora sustituimos lo que conocemos: \( 0 = 2 - \frac {10· \Delta t^2}{2} \) \( 5· \Delta t^2 = 2 \Rightarrow \Delta t_{PARCIAL} = 0,6 s\) El tiempo hasta la altura máxima es la mitad del tiempo total, esto quiere decir que si yo lo multiplico por dos, conoceré el tiempo total del proyectil en el aire. \( \Delta t_{TOTAL} = 1,2 s \) Como conozco el desplazamiento total (alcance) y el tiempo total, puedo calcular la velocidad en el eje x: \( v_{x} = \frac {\Delta x}{\Delta t} = \frac {6,0 m}{1,2 s} = 5 \frac {m}{s} \). Calcularé la velocidad inicial en el eje y: \( v_{oy} = \Delta t · g = 0,6 · 10 = 6,0 \frac {m}{s} \) La velocidad en x es constante, esto quiere decir que \( v_{x} = v_{ox} \). Ahora calcularé el ángulo de inclinación: \( tg \alpha = \frac {v_{oy}}{v_{ox}} = \frac {6,0 }{5,0 \frac {m}{s}} = 1,2 \) \( arctg (1,2) = 50º \) El ángulo con el que fue lanzado el proyectil es de 50º. Ahora calcularé la velocidad de lanzamiento: \( cos50º = \frac{5}{v_{o}} \Rightarrow v_{o} = \frac {5}{cos50º} = 7,8 \frac {m}{s} \) La velocidad de lanzamiento fue de \( 7,8 \frac {m}{s} \). |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.