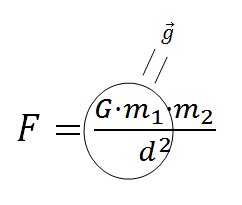La aceleración de la gravedad cerca de la superficie terrestre tiene como sabe un valor de \(g=9,8 \frac{m}{s^2}\).
a. Suponiendo a la Tierra como una esfera homogénea de 6.300 km de radio, determine la masa de la misma.
b. Determine la aceleración de la gravedad a una altura de 1.000 km sobre el nivel del mar.
|
De la ley de gravitación universal se deduce la aceleración gravitatoria terrestre:
Quote Si trabajamos con las unidades veremos que todo cierra perfectamente. 
Entonces planteamos lo siguiente:
$$ g = \frac{G·m_{T}}{r_{T}^2} $$
De aquí despejamos para aislar \(m_{T}\):
$$ m_{T} = \frac{g·r_{T}^2}{G} $$
$$ m_{T} = \frac{(9,8 \frac {m}{s^2})·(6.300.000 m)^2}{6,67·10^{-11} \frac {N·m^2}{kg^2}} $$
$$ m_{T} = 5,8·10^{24} kg $$
Ahora en la segunda parte, nos pide que determinemos la aceleración gravitatoria a los 1.000 km sobre el nivel del mar, tomaremos el radio terrestre como la distancia desde el centro del planeta Tierra hasta el nivel del mar, y le sumaremos los 1.000 km:
$$ g = \frac{G·m_{T}}{r_{T}^2} $$
$$ g = \frac{(6,67·10^{-11} \frac {N·m^2}{kg^2})·(5,8·10^{24} kg)}{(6.300.000 m + 1.000.000 m)^2} $$
$$ g = \frac{(6,67·10^{-11} \frac {N·m^2}{kg^2})·(5,8·10^{24} kg)}{(7.300.000 m)^2} $$
$$ g = 7,3 \frac {m}{s^2} $$
La respuesta es coherente, ya que cuanto más nos alejamos del planeta Tierra, la atracción de esta hacia nosotros es cada vez menor.
|