|
Cálculo de áreas
|
|
Cálculo de áreas
Toda línea cerrada o poligonal, limita cierta parte del plano que se denomina superficie. Cuando se asigna un área a una región plana, estamos asociando un número real a un conjunto que se puede medir.
Axiomas:
1. El área de una región plana es un número real no negativo.
2. El área de un rectángulo es el producto de las longitudes de dos lados consecutivos.
3. Figuras congruentes tienen áreas congruentes.
4. Si una región está incluida en una segunda, entonces, el área de la primera es menor o igual al área de la segunda.
|
Área del paralelogramo:
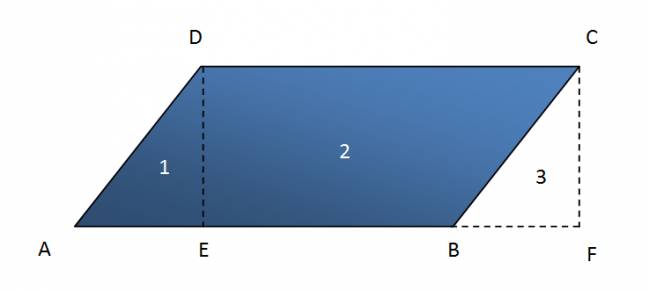
Sea \(ABCD\) el paralelogramo de la figura. Se denomina base a un lado cualquiera, y altura a la correspondiente distancia de ese lado a su opuesto. Desde los vértices \(D\) y \(C\) trazamos perpendiculares a la recta \(AB\), y obtenemos las proyecciones \(E\) y \(F\) según la figura.
Consideramos que: \( d(A, B) = d(C, D) = b \) y \( d(D, E) = h \)
Probaremos que el área del paralelogramo es: \( Á = b·h \)
Demostración:
Los triángulos rectángulos \( ADE \) y \( BCF \) son congruentes porque tienen los ángulos iguales: \( DAE = CBF \) (dos rectas paralelas cortan a una tercera determinando ángulos congruentes), \( DEA = CFB \) (ángulos rectos y las hipotenusas \(AD \) Y \( BC \) son congruentes porque son lados opuestos del paralelogramo).
Sean: \( Á_{1} = Á_{ADE}, Á_{2} = Á_{DEBC}, Á_{3} = Á_{BCF} \)
Por consiguiente, se cumple que: \( Á_{ABCD} = Á_{1} + Á_{2} \) y \( Á_{EFCD} = Á_{2} + Á_{3} \)
Como los triángulos ADE y BCF son congruentes se cumple que: \( Á_{1} = Á_{3} \)
\( Á_{ABCD} = Á_{1} + Á_{2}, Á_{EFCD} = Á_{2} + Á_{3}, Á_{1} = Á_{3} \Rightarrow Á_{ABCD} = Á_{EFCD} \)
Es decir que el área del paralelogramo ABCD es igual al área del rectángulo FEDC.
El área del rectángulo mencionado es \( d(C, D) · d(D, E) = b·h \), tendremos que e área del paralelogramo es \( Á_{ABCD} = b·h \), como se quería demostrar.
|
Área del triángulo:
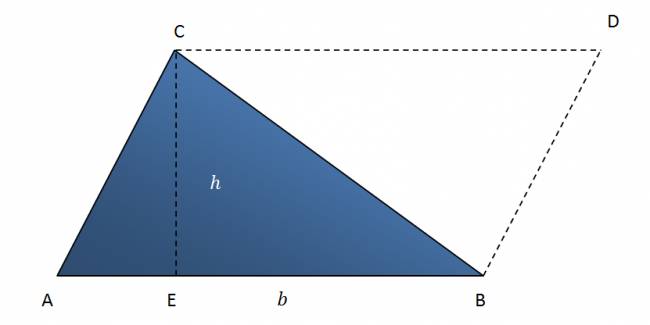
Sea el triángulo \(ABC\) de la figura. Por \(B\) y \(C\) se trazan rectas paralelas a las rectas que contienen a los lados opuestos del triángulo. Dichas paralelas se cortan en el punto \(D\). Por como fue construido el cuadrilátero \(ABDC\) es un paralelogramo. Se considera además que el punto \(E\), proyección ortogonal de \(C\) sobre la recta \(AB\).
Denominaremos \( d(A, B) = b \), y \( d(C, E) = h \).
Cada diagonal del paralelogramo divide a éste en dos triángulos congruentes (un lado en común y ángulos alternos internos iguales \(ACB = DBC\) y \(ABC = DCB\)).
Luego, el área del paralelogramo es igual a la suma de las dos áreas del los triángulos iguales:
\( Á_{ABCD} = Á_{ABC} + Á_{BCD} \Rightarrow Á_{ABCD} = 2·Á_{ABC} \)
Como el área del paralelogramo \(ABDC\) es igual a \(b·h\), se concluye que el área del triángulo es:
$$ Á_{ABC} = \frac {b·h}{2} $$
|
Área del círuclo
Como se puede ver en la siguiente animación, vemos que el área del círculo se puede descomponer en el área de un triángulo rectángulo, siendo uno de sus catetos (la base) el perímetro del triángulo y otro de sus catetos (en este caso, una altura del triángulo) el radio del círculo.
Tenemos que el área del triángulo es:
$$ Á = \frac {b·h}{2} \Rightarrow Á = \frac {(2·r· \pi)·r}{2} \Rightarrow Á = \pi · r^2 $$
|
Área de un sector del círculo:
Dados dos puntos A y B diferentes y pertenecientes a una circunferencia de centro O, queda determinado un sector de la circunferencia con los radios AO, OB y el arco AB. Sea nº la medida en grados sexagesimales del ángulo AOB.
$$ Á = \frac {(r^2· \pi)·nº}{360º} $$
Siendo:
· Á = área
· r = radio
· nº = grados sexagesimales del sector que se desea calcular
|