16-11-2012, 7:52 PM
Enunciado:
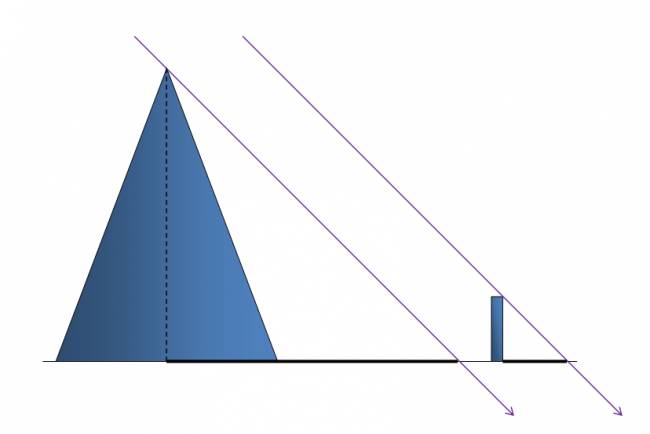
Si tres o más rectas paralelas son intersectadas por dos secantes, las longitudes de los segmentos determinados por los puntos de intersección sobre una de ellas, son proporcionales a la longitud de los segmentos correspondientes en la otra.
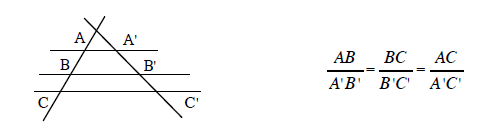
· Demostración del teorema de Thales.
División de un segmento en partes iguales por teorema de Thales:
Recíproco del teorema de Thales:
Si varias rectas son cortadas por transversales, determinando segmentos proporcionales, dichas rectas serán paralelas.
Si tres o más rectas paralelas son intersectadas por dos secantes, las longitudes de los segmentos determinados por los puntos de intersección sobre una de ellas, son proporcionales a la longitud de los segmentos correspondientes en la otra.
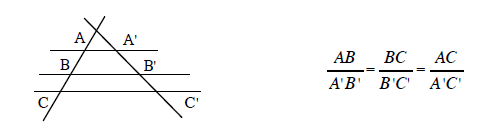
Razones y proporciones:
· Razón:
Dados en un cierto orden dos números \( a \) y \( b \), llamaremos razón al cociente obtenido al dividir a entre b.
$$ \frac {a}{b} = razon $$
Ejemplo:
Hallar la razón de dividir 12 entre 3.
$$ \frac {12}{3} = 4 $$
R: La razón es 4.
· Proporción:
Llamaremos proporción a la igualdad de dos o más razones:
Ejemplo:
$$ \frac {8}{4} = \frac {6}{x} \Rightarrow x = \frac {6·4}{8} = 3 $$
· Razón:
Dados en un cierto orden dos números \( a \) y \( b \), llamaremos razón al cociente obtenido al dividir a entre b.
$$ \frac {a}{b} = razon $$
Ejemplo:
Hallar la razón de dividir 12 entre 3.
$$ \frac {12}{3} = 4 $$
R: La razón es 4.
· Proporción:
Llamaremos proporción a la igualdad de dos o más razones:
Ejemplo:
$$ \frac {8}{4} = \frac {6}{x} \Rightarrow x = \frac {6·4}{8} = 3 $$
· Demostración del teorema de Thales.
División de un segmento en partes iguales por teorema de Thales:
Recíproco del teorema de Thales:
Si varias rectas son cortadas por transversales, determinando segmentos proporcionales, dichas rectas serán paralelas.