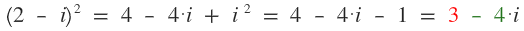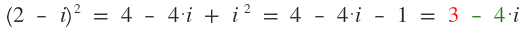Universo Científico :: Ejercicios de número complejo

Página 1 de 1
1

Ejercicios de número complejo

1. ¿Cuál es la parte real del número complejo (2 - i)²?
2. ¿Cuál es la parte imaginaria del número complejo (2 - i)²?
3. Si z = 3 + 5·i, w = -3 - 7·i, ¿cuánto es (z + w)⁵?
4. La ecuación en ℂ, x² + x + 1 = 0, tiene dos raíces: ¿opuestas, conjugadas o iguales?
5. ¿Cuál es el inverso del número complejo 1-i?
6. ¿Cuál es el cuadrado de √2 + √2·i?

1. ¿Cuál es la parte real del número complejo (2 - i)²?

Debemos desarrollar el número para la expresión para conocer el número complejo.

La parte real es: 3

2. ¿Cuál es la parte imaginaria del número complejo (2 - i)²?

Debemos desarrollar el número para la expresión para conocer el número complejo.

La parte imaginaria es: -4

3. Si z = 3 + 5·i, w = -3 - 7·i, ¿cuánto es (z + w)⁵?

Primero que nada planteamos la suma de z + w.

$$z+w=(3 + 5·i)+(-3 - 7·i)$$
$$z+w=-2·i$$

Ahora, lo que nos dio, lo elevamos a la 5:
$$(-2·i)^2=4·i^2=-4$$
$$(-4)·(-4)=16$$
$$16·(-2·i)=-32·i$$

Quote

Atención: no hice directamente todo a la quinta, sino que elevé primero al cuadrado, luego multipliqué por el mismo cuadrado, de esta forma estoy elevando a la 4 de una forma más rápida, y finalmente multiplico por lo primero, y llego a multiplicar a la 5º.

R: -32·i

4. La ecuación en ℂ, x² + x + 1 = 0, tiene dos raíces: ¿opuestas, conjugadas o iguales?

Primero que nada hay que hallar las raíces:
$$x^2 + x + 1 = 0$$
Resolvemos por la fórmula de Bháskara:
$$x={-b\pm\sqrt{b^2-4\cdot a\cdot c}\over{2\cdot a}}$$
$$x={-1\pm\sqrt{1^2-4·1·1} \over {2·1}}$$
$$x={-1\pm\sqrt{1-4} \over {2}}$$
$$x={-1\pm\sqrt{-3} \over {2}}$$
$$x_{1}={-1+\sqrt{-3} \over {2}} ∧ x_{2}={-1-\sqrt{-3} \over {2}}$$
$$S = \left\{ {-1+\sqrt{3}·i \over {2}}, {-1-\sqrt{3}·i \over {2}} \right\}$$

Quote

Podemos afirmar que las raíces de la ecuación son conjugadas.

Página 1 de 1
1

Universo Científico

marcos364

Admin

Admin

Admin

Admin