|
   |
| Foro Departamento de Matemática Teóricos Teorema de la mediana |
| Teorema de la mediana |
|
03-03-2013, 11:41 PM
Post: #1
|
|||
|
|||
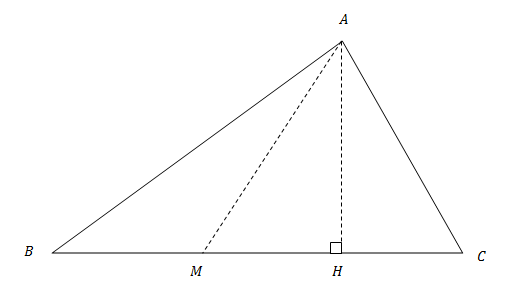
 Enunciado: El cuadrado de la longitud de la mediana de un triángulo es igual a la semisuma de los cuadrados de las longitudes de los lados que concurren al vértice la mediana, menos la cuarta parte de la longitud del lado opuesto al vértice. $$ \overline {AM}^2 = \frac {\overline {AB}^2 + \overline {AC}^2}{2} - \frac {\overline {BC}^2}{4} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
  |
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |